 |
We continue the experiment of the previous chapter, It starts after the system has reached a steady state. The system consists of two CA: CA-2 controls CA-1, while CA-1 does not control CA-2
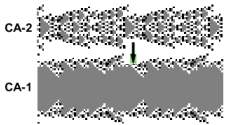 |
CA-2 cycles through its states
at a period of 46.
In the following 46 experiments the border bit of each state was
set to zero at a time.(v. Internal Injury). There
were four kinds of outcome:
1. No change,
2. A new stationary oscillating attractor.
3. Chaotic oscillations
4. Death
Here we are interested only
in the second outcome, like the one depicted below.
 |
A chaotic CA-2 induces chaos also in CA-1.
When CA-2 dies, CA-1 is released
from its control and responds
in the same way as described in the previous chapter..
Only 9% of the CA-1 survive after CA-2 dies.
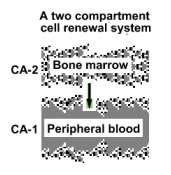
The experiment illustrates the behavior of a two compartment
cell renewal system (v.
streaming tissues), like bone
marrow and peripheral blood. The first .supplies the second with cells. Peripheral blood depends on the bone marrow product,
while the bone marrow is independent. Suppose a viral infection damages
the bone marrow, which produces
less cells and the blood becomes pale (anemia). Here damage is manifested
by irregularities of the CA. When infection is over, bone marrow regenerates
and replenishes the blood with cells. The periphery (blood) regains steady
state long after the bone marrow does.
 |
Setup