Affinity is defined here as interaction intensity. At low affinity, CA-1 is chaotic. At affinity = 2, one CA-1 border oscillates at a period 46, while the oscillation of the other border is irregular. At higher affinities CA-1 becomes broader while its product does not change. It becomes less and less healthy.

Solution

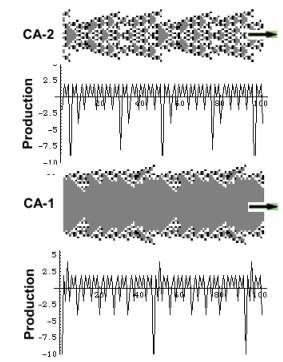A stationary process responds to external perturbation (injury) in four ways:
1. No change,
2. A new stationary oscillating attractor.
3. Chaotic oscillations
4. Death

When the CA settles at a stable  attractor, its response is regarded here as a solution which it created in response to the perturbation . A chaotic oscillation is not  a solution since it is unstable. Throughout the chaotic phase CA seeks a solution otherwise it dies. The fate of an isolated  CA is controlled by a triplet : {state, rule#, max age}.  A solution is defined as a stable quadruple: {perturbation, state, rule#, max age: stable}, which is the key feature of WOB. The body is continually exposed to perturbations for which WOB always finds (creates) an optimal solution, as manifested by Homeostasis (Homeorhesis). Homeorhesis is always an optimal solution.

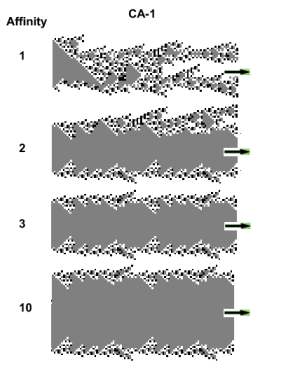
We shall therefore focus on solutions in general, and optimal solutions in particular. The last image illustrates what is meant. The first two CA are chaotic and  therefore are not solutions. CA whose affinities are 3 or greater, are solutions yet less and less optimal (healthy)

Setup
injurystate[1, j, 1, 1000, f[[2, 1]], 3. nowdat[[2,10]],1]; injurystate[1, j, 1, 1000, f[[2, 2]], 3. nowdat[[2, 10]],1];

Previous page
Next page