 |
Context of a solution
We distinguish between two kinds of solution,
depending on their context : A
solution in a narrow context, when CA rule is
constant and, a wide context solution,
when CA rule varies. An isolated CA [rule=600] is a solution of the
first kind. When parts of its rule are injured, it is driven out of
its isolation, entering a wider context
. The outcome may vary. CA may expand, or it may die. It may also take
up a stable oscillation, which is regarded here as a solution.
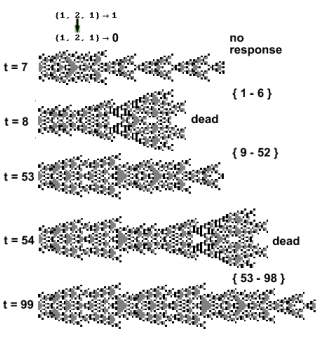
Three such solutions where depicted in a previous
experiment when the rule was injured at t = 1. The present experiment
explores what happens when the rule is injured at rising times. In the
image below, when the rule is
injured at times 1 - 6 the CA maintains its structure (does not
respond). Only at t = 7
it is driven out of its isolation, enters a short transitory
phase after which it creates a new solution. When the rule is injured
at t = 8, CA dies. Between t = 9-52 it does not respond. At t = 53 CA
starts its new cycle, whose period is 46, and
responds like at t = 7.
 |
 |
Rule injury is induced here by the observer. Imagine that
the same injuries were initiated by a CA. The three solutions depicted above
are joint creations of the two CA. They are wide context solutions. On its
own, CA[600] can never create
these solutions since they were initiated by changing the rule. Part of
the CA[600] narrow context
solution set is depicted in chapter 53
Transformation
invariance
A closer look at the non responding states reveals an interesting
CA property. Take the CA state
at t = 1 Despite interaction with three different rules, its subsequent state remains the same. Transformation
of this state was invariant under three different rules (mappings),
rule 600, and its two injured sequels.
And so are also other
non responding states.
nca=1 zygote -> effect[no 1000]; go109]; restoreparams; putinstep [ If[j > mm =20, rul1[[21,2]] = 2; rul[[1]] = rul1]; go[100]; solutions: {a. color, rule-position, time} a017mm, a221mm..
Next page