Optimality

The previous experiment demonstrated the four  types of  response by an injured  stationary process (CA) :
1. No change,
2. A new stationary oscillating attractor
3. Chaotic oscillations
4. Death

An isolated (non-interacting) process (CA) oscillates around a fixed attractor. This state is called in medicine Homeostasis (steady state). If injury does not force it from its current attractor, the CA is immune to it. Otherwise it responds with a chaotic oscillation, which may either establish a new oscillating attractor, or the CA dies. A CA does not proceed directly from one stationary attractor to another. It always traverses  first through a chaotic state.

The following experiment describes such a transition in detail  It  started in the chapter Perturbation of a Non-linear Process, when a zygote was planted and grew into a 'parent CA-1' with a period of 46 days. Next, the parent CA-1 was injured, and after a brief transition became an 'offspring  CA-2' with a period of 29 days.  In the present experiment offspring CA-2 was injured and resumed its parent phenotype (v. Memory of a Nonlinear Process)

The experiment starts at time = 0. CA-2 (offspring) oscillates with a period of 29 days. On day 57 it is injured, whereupon it enters a chaotic state which ends on day 213 when the parent CA-1 emerges (period 46).

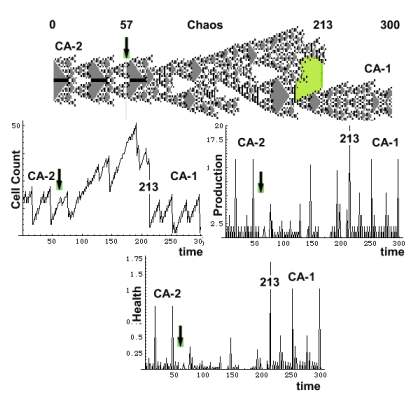The left graph depicts cell count changes. Following injury the count rises, and on day 213 it  declines abruptly. The green mask covers the white area which still belongs to the chaotic CA. When cell count reaches its peak, one of the cells becomes a zygote (blastema). As other CA-2 cells gradually disappear zygote  generates a parent CA-1.

During the chaotic phase CA production declines. On day 213 when CA-2 cells die, production rises sharply, and then declines to the CA-1 level.  Throughout the chaotic phase CA-2 is less healthy. Upon its transformation into CA-1 it health improves.

Solution

The CA repertory consists of three states, two stable attractors ,parent and offspring, and a chaotic transition.  When  perturbed, the CA  enters a chaotic phase during which it attempts to settle down at a stable attractor, which happens when  a chaotic structure matches one of the structures in the oscillating CA. The parent has 46 such structures, and when the chaotic CA takes on one of them, it enters the parent attractor. This may require time.  In this short experiment, the chances that  such an event will happen, are slim.  The CA applies its rescue repertory, and generates a blastema. 

The transition from the chaotic phase to a stable attractor is called a solution. When perturbed, the CA seeks a solution, otherwise it may die. On one hand perturbation is dangerous, since it drives the CA through an inefficient chaotic phase, when its health declines.  On the other hand, it forces the CA to seek new solutions which may improve its condition. In the present experiment injury drove CA-2 to the healthier state of CA-1. (v. Immunity)

Optimality principle

Similar transitions and responses occur also in our body. When perturbed, WOB always finds the optimal or healthiest solution under the circumstances.  This ought to be regarded as a principle that marks life and operates in all life forms. It keeps us alive!

We may now rephrase the four causes of change as follows:
1. Material cause:  CA structure, and age
2. Formal cause:  Its rule
3. Efficient cause: Perturbation (injury)
4. Final cause: Optimality

Teleology

Final cause explaines change by the purpose it may have. It is known also as teleology. This kind of explanation is rejected by Physics, since  the mechanistic world-view considers only the  efficient cause and has little room for purposefulness. Yet the final cause is essential when explaining the change of life forms, in which the purpose of change is to optimize   Suppose a well defined physical force propels an animal. Its center of mass traces a trajectory of a shotgun and obeys Newton's laws of motion. However  in the context of its body, perturbation affects myriad processes, which adjust optimally to the new situation. Unlike the projectile, which follows a four-dimensional path, the animal traces a multi dimensional trajectory. In the first four dimensions (space and time) its change is determined by the efficient cause (laws of mechanics).  while its higher dimensions are controlled by optimality, or final cause.

Setup
effect[1,500]; effect[2, 500]; injurystate[1, j, 47, f[[1,1]], 1, 0]; restoreparams[1,1,1]; restoreparams[2,2,1]; injurystate[1, j, 57, f[[1,1]], 1, 0];