 |
Memory
of a Nonlinear Process
The previous experiment depicted a
stationary oscillating CA-1 with a period of 46 days, which is called
here the parent. One of its border cells
was injured (set to zero = white), and the parent was transformed into an oscillating CA-2 with a period of 29, called here
the offspring. The offspring
was later injured in the same way as its parent before. The experiment
was repeated 29 times. Each time a different border cell was injured, and the response of the CA monitored.
30% perturbations ended in CA-2 death. 20% led to the creation
of a new attractor
with the same period and structure (phenotype) .30%
became chaotic, and 20%
assumed the parent phenotype
with a period of 46 days.
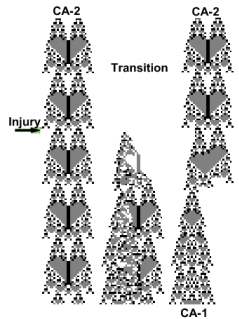
The image depicts the transition of the CA-2
offspring back to its parent CA-1 attractor. The left CA-2 was injured
and the outcome is depicted in the right CA-2. The image in between is
the absolute difference between the two CA. It shows that the perturbation
progressed from the left CA-2 border to the right. Then offspring assumed
its parent phenotype.
 |
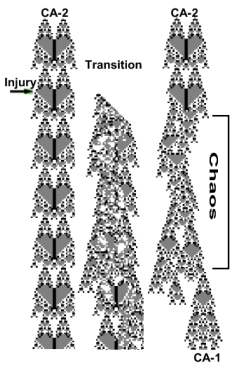
Not all transitions were so fast (short). Some perturbations initiated a prolonged chaotic behavior which occasionally settled on the parent attractor like in the image below, The experiment lasted 300 days. It is possible that later on, also other chaotic attractors may have transformed into to their parent phenotype.
 |
Memory
The experiment illustrates an interesting phenomenon. Offspring remembers
its parent phenotype, and occasionally assumes it. Where is this memory
stored? The fate of the CA
is controlled by a triplet : {state, rule#, max age}.
Here max age was set to infinite and had no effect on CA behavior.
Parent memory was stored in the structure and rule. The latter is inherited
by each cell, and may be regarded as its gene, which controls also CA structure,
or phenotype.
This simple relationship holds only in an isolated CA which
does not interact with the environment. When perturbed (injured), phenotype
is determined by gene, state, and perturbation.
The memory of this interaction
is stored in the CA structure, and was described in the chapter: Regeneration
during chronic Injury.
Change
1. Material cause:
CA structure, and age
2. Formal
cause: Its rule
3. Efficient
cause: Perturbation (injury)
4. Final
cause: To stay alive
They were defined by Aristotle (v. Chapter on CA
Creativity ), and are essential for understanding life phenomena. While
Physics can manage with efficient cause, Medicine, cannot. Its rejection
of the other causes leads to treatment induced diseases, called
Iatrogenesis.
Different kinds of Chaos
A chaotic change caused by the rule #600, will produce different oscillators
than that caused by #2058. The
outcome of a chaotic phase will thus depend on the CA rule, and since each
rule is associated with a distinct oscillator set, each CA
rule generates a different chaotic trajectory. Wolfram's rule numbering (p. 54), may
therefore be applied also to number the chaotic changes following
a perturbation. We start with a zygote ( = 1), let it grow, and set
one of its progeny to zero. Each CA type will create different chaotic trajectories
, which may be distinguished from each other by their oscillator sets. One
may regard this chaos set as a number system.
A CA may respond to perturbation in four ways:
1. No effect,
2. Oscillation
3. Chaotic change
4. Death
Actually there are two kinds of oscillation, stationary and non stationary . The latter is depicted in the chapter on Recollection. We shall be concerned with stationary processes, like the two described above. While a stationary oscillation is stable, chaos is not. Generally, injury will drive the CA from one stationary oscillating attractor to another. Chaotic response is extremely dangerous and unless it settles in an stationary attractor, CA dies.
Setup
effect[1,500]; effect[2,500]; injurystate[1, j, 47, f[[1,1]], 1, 0]; injurystate[2, j, 47,
f[[2,1]], 1, 0]; injurystate[2, j, 127, f[[2,1]], 1, 0];