Interim Summary

A CA is specified by the following formula: f[state[j, 1], rule[#], max age]
state [ j, i]:
j : another CA
i : present
rule [#] : Is totalistic (k=3, r=1), and its numbering (#) is given in Wolfram's book.
max age : Age at death

f[state[j, 1], rule[#], max age] = 1	Initialization
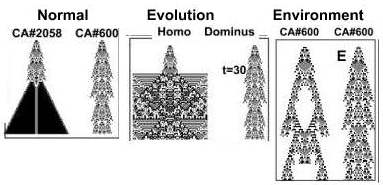
f[state[j, i], rule[#], max age] = f[state[j, i - 1], rule[#], max age]	Normal growth
f[state[j, i], rule[#], max age] = f[state[j - 1, i - 1], rule[#], max age]	CA-2 sets the state of CA-1
f[state[j, i], rule[#], max age] = f[state[j, i - 1], state[j - 1, i - 1], max age]	CA-2 sets the rule of CA-1	Evolution
f[state[j, i], rule[#], max age] = f[state[j, i - 1], rule[#], state[j - 1, i - 1]]	CA-2 sets the age at death	Environmrnt

 

Previous Page
Next page