 |
Maturation
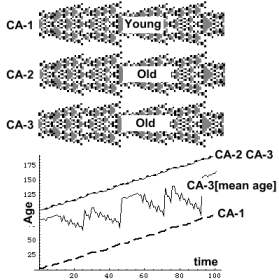
Three CA evolve side by side. Two old
and one young. The curves depict their maximal ages. Between them is
the oscillating mean age of CA-3 whose period is
46 .. The CA do not interact. Their aging velocities are equal, and
their age trajectories are parallel. At this stage the system is isolated
and its components do not interact.
It may be regarded
as a Galilean age space. Yet once CA start interacting
Galilean transformations do not hold anymore.
 |
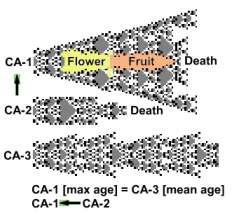 |
When our experiment begins, CA-2 matures, and starts transferring
its age (resources) to CA-1, whose
aging velocity rises, and its age approaches CA-3[mean age]. When
reaching it, CA-1 starts differentiating and produces cells. CA-2 age declines until it dies. CA-1 continues
to live for a while and then dies.
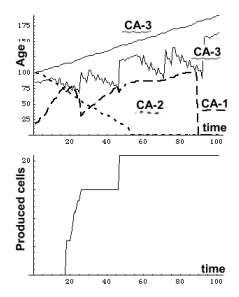 |
The experiment highlights
another aspect of the blossom model depicted
in the previous chapter. It started with three non interacting
CA with the same aging velocity. Interaction was triggered by an external
event that injured CA-2, while
here the trigger is internal . Only after accumulating enough
resources (age), CA-2 is mature enough to trigger the blossom. This simple safety mechanism assures that cells are produced
only by a mature system.
Setup
nca=3; zygote -> effect[no, 1000]; go[17];
go109]; restoreparams; effect[1,
nowdat [[3, 7]], 0]; donate[1, 2];
go [100];