 |
A Minimal Nonlinear System
The design of the present experiment is the same as in
the previous page only that both CAs interact. i ={1 , 2}. The
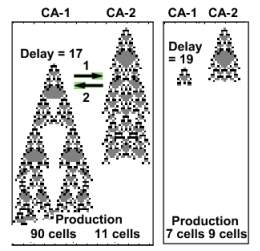
next image depicts CA structure and position at respective delays of 17,
and 19 days. Cell production during a life time of a CA is given below its
image.
 |
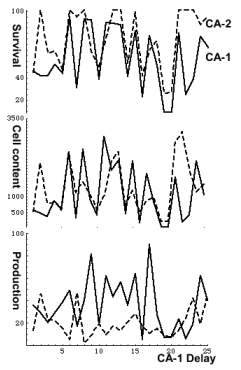
The following graphs depict survival, cell content, and daily production as a function of CA-1 delay.
 |
Efficiency
The cost of the product is determined by two factors : 1. Turnover time, and 2.
CA size (cell content) (= resources) .
The maximum of fraction
f-1 = (cell production)/ (turnover time) is at delay =17.
The maximum of fraction f-2
= (cell production)/( turnover time * cell content) is at delay = 19.
 |
This experiment illustrates what kind of problems WOB computer
is expected to compute.
Given a rule, two zygotes, and interaction I
={ j , k}. Zygote 2 is planted
at t = 0.
When to plant the first zygote so that the system will maximize cell production
at the lowest cost? You may notice that the solution is somewhat counter intuitive.
This experiment illustrates also how our WOB solves our
existence problems. WOB will always favor
a solution which requires
the smallest cost. Since many such solutions seem counter intuitive, physicians unnecessarily intervene and harm the patient.
Survival of the fittest
The f-2 graph illustrates what survival advantage might mean. You plant 25 zygote couples, each with a different CA-1 delay. When a couple dies it is replaced by a new zygote couple. After several generations the couple with a 19 delay will outnumber the others. Since its CAs are small their turnover time is short, and they need fewer resources to mature.
Further reading: